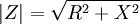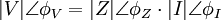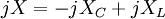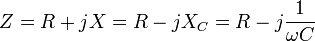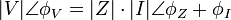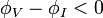Öz direnç

Empedansın grafiksel gösterimi

AC devrelerinde direncin eşdeğeri olarak empedans kavramı kullanılır. İçinde kondansatör ve endüktans gibi zamanla değişen değerlere sahip olan elemanlar olan devrelerde direnç yerine empedans kullanılmaktadır. Aşağıda görüldüğü gibi empedans, biri reel diğeri sanal iki kısımdan oluşan kompleks bir sayıdır.

$\ Z = R + jX$

Devreye bağlı bulunan saf omik dirençlerin eşdeğeri 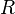$\ R$ kısmına (reel), kondansatör ve endüktansların eşdeğeri ise 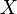$\ X$ kısmına (sanal) yazılır. Bundan sonra AC gerilimin uygulandığı devrelerde direnç ( 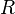$\ R$ ) yerine empedans ( $\ Z$ ) kavramı kullanılacaktır. Yani geçerli formül AC analizde aşağıdaki ifadeye dönüşür.

$\ V = Z \cdot I$

$\ Z$ bir kompleks sayı olduğundan, bir genliğe ve açıya bağlı olarak da ifade edilebilir. Aşağıdaki ifadelerle empedansın çeşitli büyüklükleri incelenebilir.	Bu bilinenler ışığında gerilimin ifadesi aşağıdaki gibi çıkartılabilir.
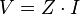
$\ Z = \|Z\| \angle \phi_Z$ $\ \|Z\| = \sqrt{R^2 + X^2}$ $\ \phi = tan^{-1} ( \frac {X}{R} )$	$\ V = Z \cdot I$ $\ \|V\| \angle \phi_V = \|Z\| \angle \phi_Z\cdot\|I\| \angle \phi_I$ $\ \|V\| = \|Z\|\cdot\|I\| \angle (\phi_Z + \phi_I - \phi_V)$

Şebeke geriliminin faz açısının 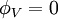$\ \phi_V = 0$ olduğunu düşünürsek ifade basitleşecektir.

$\ |V| = |Z|\cdot|I| \angle (\phi_Z + \phi_I)$

Sol tarafın faz açısı $\ 0$ ‘dır. Dolayısıyla sağ tarafın da faz açıları toplamı $\ 0$ olmalıdır. Bunun gerçekleşme şartı ise empedans ve akımın faz açılarının değer olarak birbirlerine eş, işaret olarak birbirine ters olmasıdır.

$\ \phi_V = 0 \to \phi_Z + \phi_I = 0$

$\ \phi_Z = - \phi_I$

Empedans

Kapasitif bir yükün empedansında, sanal kısım ters yönde döner ve empedansın faz açısı negatif çıkar.

Akım ve gerilim fazörlerinin birbirine göre durumu.

Kapasitif yüklerde akım fazörü gerilim fazörünün faz farkı kadar önünden ilerler.

Empedans, AC devrelerinde direncin eşdeğeridir. Direnç sadece reel kısımdan oluşan bir büyüklük olmasına rağmen, empedansın sanal kısmı bulunur. Kondansatör, ifade edilirken türev ifadesini de yanında ge
tirir ve empedans kavramının açıklanmasını gerekli kılar. Empedans aşağıdaki gibi tanımlanır.

$\ Z = R + jX$

Bu ifadede 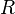$\ R$ saf direnç eşdeğerini belirtir, 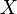$\ X$ ise devrede bulunan kondansatör ve endüktansların reaktanslarının eşdeğerini belirtir. Kondansatörün reaktansı $\ X_C$ , endüktansın reaktansı ise $\ X_L$ ‘dir. Bu durumda empedansın sanal kısmı kondansatörün üst bölümlerde açıklanan frekans domeni ifadesine göre aşağıdaki gibi olur.

$\ jX = - j X_C + j X_L$

Saf kondansatör bağlı bir devreyi inceleyeceğimizden 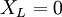$\ X_L = 0$ olarak kabul edilir ve yukarıdaki ifade aşağıdaki hale dönüşür.

$\ jX = - j X_C = - j \frac {1}{ \omega C}$

Bir direnç ve bir kondansatörün bağlı olduğu devre göz önüne alındığında empedans, aşağıdaki gibi olur.

$\ Z = R + jX = R - j X_C = R - j \frac {1}{ \omega C}$

Bu ifade bize oldukça fazla bilgi verir. Empedansın içerisinde sanal kısmın önünde bulunan $\ +$ işaret $\ -$ ‘ye dönüştü. Bu da yandaki empedans diyagramında olduğu gibi kapasitif reaktansın ters yönde dönmesine neden olur. Dolayısıyla, kondansatör empedansının faz açısı negatif yönde çıkar. Aşağıdaki grafikten de kapasitif bir yükün empedansının fazör diyagramı görülür.

$\ V = Z \cdot I$

$\ |V| \angle \phi_V = |Z| \cdot |I| \angle {\phi_Z + \phi_I}$

Bu ifadeden anlaşılan, gerilimin faz değerinin, akımla empedansın faz değerlerinin toplamı olduğudur. Kapasitif devrede empedansın faz değeri negatif olduğundan aşağıdaki eşitlikler çıkartılır.

$\ \phi_V = \phi_Z + \phi_I$

$\ \phi_V - \phi_I = \phi_Z$

$\ \phi_V - \phi_I < 0$

Son ifade akımın faz açısının gerilimin faz açısından büyük olduğunu ifade etmektedir. Yani akım fazörü, gerilim fazörüne göre önde ilerler. Kapasitif devrelerde akım gerilimden ileridedir ve empedansın sanal kısmı negatif değer alır.

"http://tr.wikipedia.org/wiki/%C3%96z_diren%C3%A7"’dan alındı

Elektro Teknoloji

Empedans Nedir ? ( Öz direnç )

Öz direnç

Empedans

Bir cevap yazın Cevabı iptal et